Совокупность всех или части условий любой задачи, оформленная в виде некоторого предиката над наборами входных данных и возможных результатов, назовем характеристическим свойством задачи. Если в предикате задействованы все условия задачи, то характеристическое свойство и соответствующий предикат назовем полным, если нет, - частичным. Формальная запись полного или частичного предиката, с одной стороны, позволяет проводить независимую “экспертную” проверку правильности работы ранее разработанных алгоритмов решения данной задачи, а с другой стороны, может оказать существенную помощь для отыскания новых рекурсивных алгоритмов её решения. Остановимся на примерах, иллюстрирующих второй вариант использования характеристических свойств задачи. Заметим, что построенные на их основе алгоритмы уже не нуждаются в доказательстве их правильности.

A. p-ичный порядок. Определим p-ичный порядок натурального числа N, то есть наибольший целый показатель степени с основанием p, на которую делится N.

В теории чисел p-ичный порядок N принято обозначать через ord_p(N). Для вычисления целого неотрицательного числа

характеристическое свойство набора (a, p, N), удовлетворяющего соотношению (3), может быть задано предикатом

Q(a, p, N) = (N º 0 (mod p^a)) Ù Ø ( N º 0 (mod p^a+1).

Так как при N º 0(mod p) и натуральном a справедливо тождество:

(N º 0(mod p^a)) Ù Ø ( N º 0(mod p^a+1) =

= ((N/p) º 0(mod p^{a- 1})) Ù Ø ((N/p) º 0(mod p^a),

то для Q(a, p, N) имеем следующее рекурсивное соотношение:

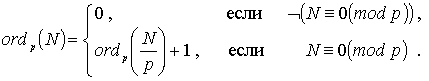
Соответствующая программа вычисления ord_p(N) могла бы выглядеть так:

Контрольные примеры:    ord(2, 100) = 2,     ord(3, 405) = 4.

B. Допустимые последовательности. Последовательность Â длины N, составленная из символов 0 и 1, называется допустимой, если в ней нет двух подряд идущих символов 1. В противном случае Â называется недопустимой. Определим K(N) - общее количество допустимых последовательностей.

Методом полного перебора эту задачу можно решить лишь при небольших значениях N, так как количество всевозможных последовательностей (наборов) равно 2^N. Пусть набор представлен в виде вектора v с компонентами 0 и 1 (с нумерацией их от 0 до N-1). Определим предикат P(v), истинный только на допустимых наборах v. Формализованная запись этого предиката выглядит следующим образом:

P(v) = (" (0 £ i £ N-2)) (Ø ((v_i = 1) Ù (v_i+1 = 1))) =

=(" (0 £ i £ N-2)) ((v_i = 1) Ù (v_i+1 = 0) Ú (v_i = 0) Ù (v_i+1 = 0) Ú (v_i = 0) Ù (v_i+1 = 1)) =

=(" (0 £ i £ N-2)) ((v_i+1 = 0) Ú ((v_i+1 = 1) Ù (v_i = 0))) =

=((" (0 £ i £ N-3)) ((v_i+1 = 0) Ú ((v_i+1 = 1) Ù (v_i = 0)))) Ù 

Ù ((v_N-1 = 0) Ú ((v_N-1 = 1) Ù (v_N-2 = 0))) =

=(((" (0 £ i £ N-3)) ((v_i+1 = 0) Ú ((v_i+1 = 1) Ù (v_i = 0)))) Ù (v_N-1 = 0)) Ú 

Ú (((" (0 £ i £ N-3)) ((v_i+1 = 0) Ú ((v_i+1 = 1) Ù (v_i = 0)))) Ù ((v_N-2 = 0) Ù (v_N-1 = 1))).

Фактически формальными преобразованиями предиката мы получили его декомпозицию, то есть нам удалось множество M(N) допустимых векторов длины N (N³3) представить в виде объединения двух непересекающихся подмножеств:

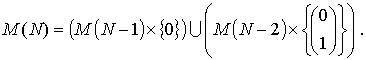
Здесь под декартовыми произведениями M(N-1)´{0} и M(N-2)´{(0, 1)^T} понимаются множества векторов длины N. В первом случае последняя компонента векторов равна 0, а первые N-1 компонентов составляют допустимые векторы длиной N-1. Во втором случае последние две компоненты равны соответственно 0 и 1, а первые N-2 компоненты составляют допустимые векторы длины N-2. Кроме того: M(1)={(0), (1)}; M(2)={(0,0)^T, (0,1)^T, (1,0)^T}. Отсюда вытекает справедливость следующего рекуррентного соотношения:

K(1) = 2,    K(2) = 3,    K(N) = K(N-1) + K(N-2)    (N ³ 3).

Таким образом, K(N) = F(N+2), то есть искомая последовательность K(N) есть сдвиг последовательности Фибоначчи F(N) на два элемента влево. Для вычисления K(N) можно написать рекурсивную программу-функцию или воспользоваться конечной формулой Бине. В первом случае решение можно задать следующей парой функций ff(N, a, b) и K(N):

Во втором случае, воспользовавшись формулой Бине для вычисления N-го члена Фибоначчи, получим:

Контрольные примеры: