
![]()
Часто в условиях задачи не только не проглядывается рекурсия, но и сама задача не является алгоритмически сформулированной. Иногда её простая перефразировка, а чаще построение математической модели позволяют вдруг обнаружить первоначально скрытую рекурсию.
A.
Динамика вклада. Большой выбор простых содержательных задач, допускающих изящное рекурсивное решение, можно встретить в сфере банковской деятельности. Ниже речь идет об обычных вкладах и сложных процентах. Рассмотрим несколько различных рекурсивных вариантов решения многим знакомой задачи о динамике вклада.Вкладчик положил в банк сумму в
sum денежных единиц под p процентов за один период времени (год, месяц, неделя и т. д.). Составим программу-функцию, возвращающую величину вклада по истечении n периодов времени (n=1, 2, …).Пусть
invest(sum,p,n) - искомая функция. Вычисления значений invest() можно проводить по известной формуле сложных процентов: invest(sum,p,n)= sum× (1+p/100)n. Однако нас будет интересовать рекурсивный вариант алгоритма решения задачи. Её параметризация реализована в постановке. Далее, если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Тем самым база рекурсии очевидна. Декомпозицию будем осуществлять по параметру n исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n- 1 период, взять и снова положить на 1 период. Фактически вместо исходной задачи предложено рассмотреть её некоторый эквивалентный переформулированный вариант. Соответствующая программа-функция могла бы выглядеть так:Реализуя декомпозицию иным способом, получим другой вариант рекурсивной программы (1):
Здесь декомпозиция проводится, исходя из такого факта. Положить некоторую сумму в банк на
n периодов – это то же самое, что положить эту сумму на 1 период, взять и снова положить на n- 1 период.В данной и подобной ей задачах указанные декомпозиционные посылки программно реализуются приблизительно с равной степенью сложности, и тем самым обе имеют право на существование. Однако может возникнуть ситуация, когда предпочтение должно быть отдано той или иной конкретной посылке. Например, если в последующем имеется необходимость перейти к нерекурсивному варианту программы, то лучше пользоваться посылкой первого типа, а если есть проблемы с доказательством правильности реализуемого алгоритма, то целесообразно работать с посылкой второго типа.
Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении
invest(sum,p,n) и invest1(sum,p,n) равно n. Можно было бы уменьшить это значение до величины floor(log2(n))+1 исходя из следующих двух декомпозиционных посылок.|
Пусть сумма sum = m × g денежных единиц помещена на вклад при ставке в p процентов за период. Тогда через n периодов sum возрастет до той же самой величины, что и совокупная сумма m отдельных вкладов по g денежных единиц каждый, также помещенных под p процентов за период. Не ограничивая общности, величину sum можно считать целым неотрицательным числом. В противном случае можно было бы перейти к иному номиналу денежных единиц. Значения m и g также будем считать целыми числами. | |
|
Положить некоторую сумму sum в банк на n периодов – это то же самое, что положить эту сумму на k (0 £ k £ n) периодов, взять и снова положить на n-k периодов. |
Основанную на этих посылках рекурсивную функцию для решения поставленной задачи обозначим через
inv(sum,p,n). Указанные посылки обнаруживают следующие свойства этой функции.Первая посылка:
inv(sum,p,n)=inv(m× g,p,n)=g× inv(m,p,n). В частности, при m=1 получаем: inv(sum,p,n)=sum× inv(1,p,n).Первая и вторая посылки. Пусть
k=floor(n/2), тогдаinv(sum,p,n)=inv(inv(sum,p,k),p,n- k)=
=inv(sum,p,k)× inv(1,p,n- k)=sum× inv(1,p,k)× inv(1,p,n- k).
Отсюда при
n=2× k сразу же получаем: inv(sum,p,n)=sum× (inv(1,p,k))2. При n=2× k+1 имеемinv(sum,p,n)=inv(sum,p,2× k+1)=
=inv(sum× (1+p/100),p,2× k)=sum× (1+p/100)× (inv(1,p,k))2.
Выведенные соотношения для
inv()позволяют записать такую программу для её вычисления:Общее количество рекурсивных вызовов при счете по этой программе-функции можно было бы подсчитать с помощью следующей вспомогательной рекурсивной функции:
и оно действительно равно
floor(log2(n))+1 (n³ 1).Незначительная перестройка структуры функции
inv(sum,p,n) позволяет получить еще один вариант её реализации, в котором количество рекурсивных вызовов в точности равно floor(log2(n))+1 (n ³ 1). Сделать это можно так:B.
Периодическое продолжение. Составим рекурсивную программу, которая для функции g(x), определенной при x Î [a,b), строит функцию peri(g,a,b,x), являющуюся периодическим продолжением g(x) на всю действительную ось c периодом w = b – a.Нам, очевидно, требуется определить функцию следующего вида:
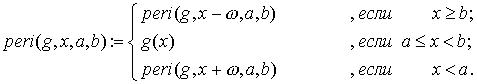
Проведенное “перефоррмулирование” задачи позволяет сразу же увидеть и рекурсию, и её базу и, наконец, декомпозицию задачи. Соответствующая программа-функция будет выглядеть так:
Заметим, что, при
x, находящемся вдали от промежутка [a,b), вычисление значения функции peri() требует значительного количества рекурсивных вызовов. Происходит это по той причине, что, за один такой вызов, мы продвигаемся в направлении к [a,b) лишь на расстояние w =b- a.Значительно эффективней проводятся вычисления по функции
F(g,x,a,b), также являющейся периодическим продолжением g(x) на всю числовую ось: Контрольные примеры:A. Пусть
y(x)=x2× sin(x). Тогда:peri(y, 1, 0, 2) = 0.841, peri(y, 3, 0, 2) = 0.841,
peri(y, -1, 0, 2) =0.841, peri(y, 1001, 0, 2) = 0.841.
B. На рисунке 6 изображен график функции
H(t), являющейся периодическим продолжением функции y(x)=x2 × sin(x) для xÎ [-10, 0). График H(t) построен с помощью программы-функции F() и выведен на промежутке [-10,20) с шагом h=0.1.t := -10, -9.9, …, 20 ; H(t) := F(y, t, -10, 0).
Рис. 6. Периодическое продолжение функции y(x)=x2 × sin(x) для xÎ [-10, 0)
![]()