Иногда удается непосредственную увидеть рекурсию в определении данных задачи или в алгоритме её решения. Иными словами условия не просто задают постановку задачи, но делают это рекурсивно. Отсюда и рекурсивные программы, во многом являющиеся копией условий задачи. Рассмотрим примеры.
Пусть одномерный массив вещественных или комплексных чисел vp (p=0, 1, …, n-1; n³1) задан компонентами вектора v=(v0, v1, … ,vn-1)T.A. Сумма n слагаемых. Составим рекурсивную программу-функцию, возвращающую сумму S компонентов вектора v: S=v0+v1 +…+vn-1. Определение суммы n слагаемых в виде:
S = v0 + v1 + … + vn-1 = (v0 + v1 + … + vn-2) + vn-1
рекурсивно по своей сути. Сумма n слагаемых есть сумма первых (n-1)-го слагаемого плюс последнее слагаемое. Этот факт и положен в основу определения функции summa(v), где v=(v0, v1, … ,vn-1)T:
Заметим, что декомпозицию можно провести и из такого представления суммы:
S=v0+v1 +…+vn-1=(v0+v1 +…+vk)+(vk+1+…+vn-1) (k=floor((n-1)/2)).
Соответствующая рекурсивная функция sum(v) могла бы выглядеть так:
И хотя в данном случае вычисления по функции sum(v) не являются более эффективными, чем по summa(v), подобная дихотомия иногда себя вполне оправдывает, существенно уменьшая общее количество рекурсивных вызовов и улучшая временные характеристики алгоритма.
B. Произведение n сомножителей. Составим рекурсивную программу-функцию, возвращающую произведение P компонентов вектора v: P= v0× v1× …× vn- 1. Определение произведения n сомножителей в виде: P= v0× v1× …× vn-1=(v0× v1× …× vn-2)× vn-1, как и соответствующее определение суммы, рекурсивно по своей сути. Произведение n сомножителей есть произведение первых (n-1)-го сомножителей, умноженное на последний сомножитель. Отсюда и определение функции product(v), где v=(v0, v1, … ,vn-1)T:
С. Произведение биномов. Составим рекурсивную программу-функцию, возвращающую коэффициенты многочлена g(x), который получается в результате перемножения биномов (x - vk) (k = 0, 1, …, n-1; n³1):
g(x)=(x- v0)× (x- v1)× …× (x- vn-1).
Будем считать, что свободные члены биномов заданы в виде компонентов некоторого вектора v=(v0, v1, … ,vn-1)T, а результат вычислений должен возвращаться также в виде вектора. Поскольку
g(x)=[(x- v0)× (x- v1)× …× (x- vn-2)]× (x- vn-1).
то несложно организовать рекурсию по количеству перемножаемых биномов. Соответствующая программа-функция могла бы выглядеть так:
Контрольный пример:
t := (1 -5 2)T , probin(t)T = [1 2 -13 10].
Замечание. Пусть по известным корням c1, c2, …, cn унарного многочлена f(x) степени n требуется найти его коэффициенты a1, a2, …, an: f(x) = xn+a1× xn-1+…+an-1× x+an. Унарность f(x) означает, что коэффициент при старшей степени x равен единице. Этим обеспечивается единственность решения поставленной задачи и коэффициенты ak (k = 1, 2, …, n) можно находить, например, с помощью формул Виета:
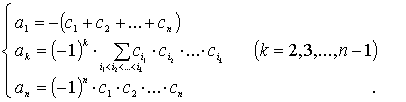
Однако конкретные вычисления по этим красивым формулам проводить затруднительно. Проще это делать с помощью рекурсивной функции probin(c), где с - вектор из корней f(x): c = (c1, c2, …, cn)T. А возможность эта вытекает из представления f(x) = (x - c1)× (x - c2)× … × (x - cn).
D. Разрезание прямоугольника на квадраты. Дан прямоугольник, длины сторон которого a и b представляют собой натуральные числа. Составить рекурсивную программу-функцию, подсчитывающую, на сколько квадратов с натуральными длинами сторон можно разрезать исходный прямоугольник, если каждый раз от него отрезать квадрат максимально возможной площади.
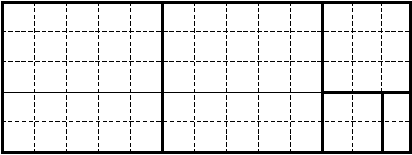
В качестве базы рекурсии можно взять случай b=0. Если numsq(a,b) - функция, возвращающая решение задачи при заданных длинах a и b (b¹ 0) сторон исходного прямоугольника, то в любом случае имеем декомпозицию:
numsq(a,b) = floor(a/b) + numsq(b, mod(a,b)).
Отсюда окончательно получаем:
Контрольные примеры: numsq(13,5) = 6, numsq(5,13) = 6.
Пусть в качестве решения задачи требуется выдать не только количество получающихся квадратов, но и размеры каждого из них. Более точно, должен быть возвращен двумерный массив ma[i, j] (i = 0, 1, ..., k; j = 0, 1), где ma[i, 0] - длина стороны очередного квадрата, а ma[i, 1] - количества квадратов со стороной ma[i, 0]. Соответствующая рекурсивная программа-функция могла бы выглядеть так:
Заметим, что nums(a, b) всегда возвращает матрицу, в последней строке которой находятся нули.
Контрольный
пример: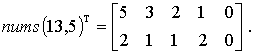 
E. Центр тяжести многоугольника. Пусть n-угольник Q задан своими вершинами Qk и q = (qi,k) (i = 0, 1; k = 0, 1, …, n-1; n³1) - матрица их прямоугольных координат: Qk = (q0,k, q1,k) (k = 0, 1, …, n-1). Составим рекурсивную программу-функцию определения координат центра тяжести O многоугольника Q.
Будем исходить из такого рекурсивного определения центра тяжести многоугольника, согласующегося с физическим понятием центра тяжести системы материальных точек:
 |
центр тяжести отрезка (двуугольника) Q = Q0Q1 есть середина отрезка [Q0,Q1] (база рекурсии); |
|
центр тяжести n-угольника Q0Q1…Qn-2Qn-1 строится так. Пусть уже построена точка P - центр тяжести (n-1)-угольника Q0Q1…Qn-2. Тогда искомый центр тяжести O есть точка отрезка [P,Qn-1], делящая его в отношении (n-1):1, считая от вершины Qn-1 (декомпозиция задачи). |
Из рекурсивности конструктивного определения понятия центра тяжести O многоугольника Q сразу же возникает справедливость следующего рекурсивного алгоритма вычисления координат O:
Контрольные примеры:
F. Моделирование испытаний. Одной
из наиболее простых и вместе с тем весьма
распространенных схем повторения
независимых испытаний является
классическая схема Бернулли. Суть её в
следующем. Пусть при некотором испытании
событие A
может наступить или не наступить. Обозначим
вероятность наступления события A
через p=p(A)
(0<p<1), а вероятность ненаступления A,
то есть противоположного события 
,
через q=1-p. Требуется определить вероятность P(n,m)
наступления события A
в серии из n
независимых испытаний ровно m
раз. Известно, что 
,
где 
-
число сочетаний из n
элементов по m.
В связи со схемой Бернулли можно поставить
много разных задач. Одной из них, весьма
необычной и поучительной с точки зрения
рекурсивной реализации её решения, мы и
займемся. Сформулируем её в двух вариантах: F1
и F2.
F1. Составить рекурсивную программу-функцию, которая для данного события A и его вероятности p наступления при каждом испытании моделирует схему Бернулли и подсчитывает значение случайной величины x, равной количеству появлений A до первой неудачи.
F2. Составить рекурсивную программу-функцию, решающую задачу F1 последовательно n раз и возвращающую результат в виде компонентов вектора.
Начнем с решения задачи F1. Появление или непоявление события A в схеме Бернулли легко моделируется датчиком случайных чисел. Например, функция rnd(a) (a>0) возвращает равномерно распределенное случайное значение x: 0£ x<a. Поэтому вне зависимости от сути события A очередное полученное по rnd(1) значение можно интерпретировать так:
0£ rnd(1)<p « событие A наступило,
p£ rnd(1)<1 « событие A не наступило.
Исходя из сказанного, для решения подзадачи F1 можно предложить такую функцию:
Здесь ненаступление события A определяет терминальную ветвь vmat() и, следовательно, служит базой рекурсии. Декомпозиция задачи состоит в простом переходе к следующему испытанию. Фактически мы имеем рекурсивное определение серии испытаний до первой неудачи. В чем же необычность “вероятностной рекурсии”? Функция обращается сама к себе с тем же самым значением аргумента p, а проблема остановки алгоритма решается вовсе не за счет изменения её аргумента, а за счет внешнего датчика, то есть получения конкретных значений другой вспомогательной функции. В данном случае это функция rnd(1), которая, по сути, является неявным аргументом функции vmat(p).
Умея решать задачу F1, для решения задачи F2, то есть получения “серии серий” испытаний до первой неудачи, можно предложить такую функцию:
Случай n=1 является базой рекурсии, а далее мы имеем простую повторительную рекурсию.
Контрольный пример:
v := mas(9 0.8), vT=[1 8 10 0 2 6 2 4 3].
G. Вложенные массивы. В некоторых языках программирования допускаются массивы, элементы которых снова могут быть массивами и т. д. Подобные структурные образования данных называются вложенными (гнездовыми, вставленными) массивами.
Пример 1. Ниже в первой строке определяется вложенный массив v, а во второй строке выводятся его элементы. В векторе v в фигурных скобках указаны размеры соответствующих элементов-массивов ({строк, столбцов}), а сами элементы приведены справа от v:
Вложенные массивы можно интерпретировать в виде деревьев с корнем, являющимся основным массивом. От него идут дуги к массивам-элементам и т. д. Листьями подобного дерева являются массивы или скаляры, не имеющие ссылок на последующие массивы. Высотой вложенного массива назовем высоту соответствующего ему дерева (максимум из количества дуг по каждому из путей от корня до листа). На рисунке 5 указано дерево составного массива, определенного в примере 2.
Пример 2.
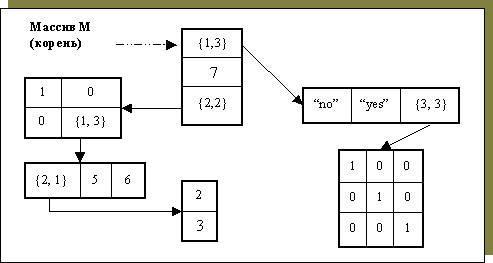
Рис. 5. Схема дерева составного массива M (пример 2)
В связи с вложенными массивами будем решать задачу рекурсивного определения их высоты. Для единообразия удобно считать векторы длины n двумерными массивами размера n´1. В этом случае нам придется иметь дело только с матрицами или скалярами. Заметим, что для опознания скаляров M в программе можно использовать встроенные функции rows(M) или cols(M), возвращающие для них нуль. Для матриц M rows(M) и cols(M) возвращают соответственно количество строк и столбцов M. С учетом сказанного рекурсивная функция нахождения высоты составного массива могла бы выглядеть так:
Аргументом hei(M) является скаляр или матрица. Если M - скаляр, то hei(M) возвращает –1. В противном случае первое рекурсивное обращение направляет вычисления по всем дугам дерева, порожденным каждым из элементов M. Углубление на каждый следующий уровень дерева в отложенных вычислениях приводит к увеличению h на 1. Но поскольку начальное значение h=-1, то, в конце концов, h примет значение не количества уровней дерева, а его высоты. В частности, если исходный массив не является вложенным, то есть состоит из скаляров, то h=0.
Контрольные примеры:
A. Для вектора v из примера 1: hei(v)=1;
B. Для матрицы M из примера 2: hei(M)=3.
Замечание. При дополнительных сведениях о вложенных массивах программу hei() можно упростить. Например, если известно, что на любом уровне вложенного массива M элементами могут быть только скаляры или векторы длины 2, то M порождает бинарное дерево и его высота может быть найдена с помощью такой простой рекурсивной функции:
Кстати, сгенерировать случайный вложенный массив, порождающий бинарное дерево со скалярами или векторами длины 2 на всех уровнях, можно по такой рекурсивной программе:
Величина параметра p (0<p<1) вероятностно влияет на высоту формируемого массива. Как правило, чем больше p, тем больше высота массива. Обычно при p³0.7 она уже становится запредельной, то есть бинарное дерево массива сильно разрастается и происходит останов вычислений по переполнению стека рекурсивных вызовов. При первом обращении к tree(p) формируется основной массив (корень дерева). Каждая его компонента генерируется независимо от другой и фактически по одной и той же схеме:
0£ rnd(1)<p « создается ссылка вида {2,1}, то есть составной массив;
p£ rnd(1)<1 « создается скаляр - 0, то есть ветвь обрывается.
Этот процесс рекурсивно продолжается с каждым из компонентов основного массива и т. д. Необычность такой рекурсии состоит в том, что функция обращается сама к себе с тем же самым значением аргумента. При этом, проблема перемещения по рекурсивным уровням, как и в примере F, решается типичным для “вероятностной” рекурсии образом - не за счет изменения аргумента функции, а за счет величины значения, получаемого от датчика случайных чисел.
