
Если для представления компонентов вектора-массива v вместо бинарного дерева использовать тернарное дерево, то можно ввести в рассмотрение понятие тернарной пирамиды. А это, в свою очередь, даст возможность построить так называемый алгоритм тернарной пирамидальной сортировки, который во многом подобен ранее рассмотренному алгоритму бинарной пирамидальной сортировки, но отличается от него лучшими характеристиками быстродействия. Мы этого делать не будем, а сразу начнем с решения более общей задачи. Введем понятие s-арных деревьев и s-арных пирамид (s = 2, 3, 4, …), на их основе построим s-арные пирамидальные сортировки, или s-сортировки, и обсудим сравнительный анализ характеристик их быстродействия при различных значениях s.
S-арным деревом будем называть ориентированный граф с n вершинами (узлами):
v0, v1, ... , vn-1. (17)
в котором v0 - корень и для всех вершин vm (m = 0, 1, ..., n-1) прямыми потомками являются следующие узлы:

Вершины, имеющие потомков, называют родителями. Будем считать, что все родители напрямую соединены направленными дугами с каждым из своих потомков (стрелки от родителя к потомкам).
Из этого определения вытекает, что корень дерева v0 с помощью дуг связан с любой другой вершиной дерева.
Говорят, что вершина v0 расположена на нулевом уровне, а вершина x¹v0 расположена на уровне q, если v0 и x соединяют q промежуточных дуг. Номером вершины vj (0 £ j £ n-1) назовем значение индекса j. Общее количество уровней без единицы, равное в нашем случае максимальному номеру уровня, называют высотой s-дерева. Пример бинарного дерева (s=2) с двенадцатью вершинами и высотой, равной 3, приведен на рис.1.
Понятие S-арной пирамиды можно дать по аналогии с соответствующим понятием бинарной пирамиды следующим образом.
S-арной пирамидой, или s-пирамидой, массива (17) называется непустая подпоследовательность его компонентов вида
vp, vp+1, ... , vq (0 £ p £ q £ n-1), (18)
для которой выполнено одно из следующих условий:
1. s × p + 1 > q;
2. s × p + 1 £ q и vj ³ vs×j+1 для p £ j £ (q-1)/s,
vj ³ vs×j+2 для p £ j £ (q-2)/s,
... ... ... ... ... ... ...
vj ³ vs×j+s для p £ j £ (q-s)/s.
Пример бинарной пирамиды (s=2) приведен на рис.2. Из определения пирамиды вытекают такие утверждения:
|
Для всякой последовательности (17) любой фрагмент её “хвостовой части”, то есть подпоследовательность |
vp, vp+1, ... , vn-1 ( p ³ ë(n + s - 2) / sû), (19)
является
пирамидой.
Если (17)
представлена в виде s-арного дерева, то его
высота равна ëlogs((n
- 1)×(s -
1)
+ 1)û
и пирамида (19) при p
= ë(n
+ s - 2) / sû
соответствует всем листьям,
то есть “висячим”,
не имеющим потомков, вершинам (см. леммы 1 и
2).
|
Если последовательность (17) - пирамида, то справедливо соотношение |
v0 = max(v0, v1, ... , vn-1). (20)
|
Последовательность (17), представленная в виде s-арного дерева, является пирамидой тогда и только тогда, когда значение любого узла j дерева не меньше значений всех его возможных непосредственных потомков: s×j + k (k = 1, 2, … , s). |
Этап 1. Построение s-пирамиды. В (17) “хвост”, то есть подпоследовательность (19) при p = ë(n + s - 2) / sû, как мы уже отмечали, является s-пирамидой. Будем наращивать (19), добавляя к ней оставшиеся элементы из (17). Пусть последовательность vj+1, vj+2, ... , vn-1 - уже s-пирамида. Припишем к ней слева элемент vj:
vj, vj+1, ... , vn-1 (2
1) и преобразуем (21) снова в s-пирамиду. Для этого “просеем” vj по соответствующей веточке представления (17) в виде s-арного дерева. Делаем это так. Рассмотрим vj и m его потомков: vs×j+1, vs×j+2, ..., vs×j+m (1£ m £ s). Если vj не меньше потомков или не имеет их, то вычисления прекращаем. В противном случае обмениваем значения vj и max(vs×j+1, vs×j+2, ..., vs×j+m) в соответствующих позициях дерева и “опустившийся” элемент продолжаем просеивать тем же самым способом. В конце концов, преобразованная последовательность (21) станет s-пирамидой. Продолжая наращивание (21), мы превратим весь массив (17) в s-пирамиду. При этом окажется выполненным равенство (20). Объявляем полученную s-пирамиду T текущей и переходим к следующему этапу. Этап 2. Сортировка s-пирамиды. В текущей s-пирамиде T начальный элемент не меньше остальных. Поступим с ним так. Обменяем значениями концевые элементы T и укоротим T справа на один элемент. Полученная последовательность уже может и не быть s-пирамидой. Применим в ней к элементу v0 процесс “просеивания”, описанный на этапе 1. Преобразованная последовательность становится s-пирамидой. Повторяя этот этап n-1 раз, отсортируем T по неубыванию.![]() адача
5.
Составить рекурсивную программу бинарной
пирамидальной сортировки массива,
заданного вектором v = (v0
v1 ... vn-1).
адача
5.
Составить рекурсивную программу бинарной
пирамидальной сортировки массива,
заданного вектором v = (v0
v1 ... vn-1).
Решение. Явное подобие предложенного выше алгоритма с алгоритмом бинарных пирамидальных сортировок позволяет сразу же записать его рекурсивный вариант в следующем виде:
Вспомогательная рекурсивная функция shifts(v, b, e, s) просеивает в векторе v компонент от позиции b и не далее чем до позиции e или, при представлении v в виде бинарного дерева, от вершины b до вершины e. При этом используется такой алгоритм. Если значение в b не меньше значений в вершинах-потомках, то вычисления прекращаются. В противном случае своими значениями обмениваются b и потомок с наибольшим значением. Если имеются несколько претендентов на обмен с b, то берется потомок с меньшим номером. Далее задача рекурсивно решается на новом участке [b, e] c измененным значением индекса b, где b¬s×b+m для некоторого m=1, 2, …, s. Базой рекурсии является условие s×b+1>e. Декомпозиция организуется по длине участка [b, e]. Функция shifts(v, b, e, s) в дальнейшем будет использоваться для восстановления в векторе v s-пирамиды на [b, e] при условии, что свойства s-пирамиды на этом участке нарушены только в вершине b.
Рекурсивная функция builds(v, k, e, s) на участке [0, e] строит в векторе v s-пирамиду. Предполагается, что на участке [k+1, e] в v s-пирамида уже построена. Рекурсия организована по параметру k.
Рекурсивная функция sortpirams(v, e, s) на участке [0, e] в векторе v сортирует ранее построенную s-пирамиду по неубыванию. Рекурсия организована по параметру e.
Головная функция piramidas(v, s), используя функции builds() и sortpirams(), строит из вектора v s-пирамиду, а затем сортирует её по неубыванию.
Незначительные изменения функции shifts() и полная реорганизация головной функции piramidas(v) для самостоятельной реализации действий, предусмотренных функциями builds() и sortpirams(), позволяют получить достаточно компактный нерекурсивный вариант алгоритма s-арной пирамидальной сортировки (s=2, 3, 4, …):
Реализация предложенного алгоритма сортировки требует по порядку не более (s + 1)×(n - 1)×logs(n×(s - 1)) операций сравнения и перемещения (см. главный член оценки в лемме 2).
Просчет контрольных примеров c помощью функции piramis(v, s) для разных n и s показал, что для широкого диапазона значений n сортировки s-пирамидами при s>2 более эффективны по сравнению с бинарными сортировками. При этом оптимальное значение s, как правило, лежит в диапазоне от 4 до 10 и выигрыш по времени для него достигает 30 процентов. Однако эти достаточно интересные экспериментальные результаты были получены в интерпретирующей среде Mathcad, а потому они вряд ли могли служить основанием для высказывания более или менее правдоподобных общих гипотез относительно быстродействия s-сортировок для разных s. И все же эта весьма неожиданная информация заставила нас провести более тщательный экспериментальный анализ s-сортировок [20, c.25-39]. На языке Object Pascal (Delphi 5) был создан соответствующий программный проект ‘Delphi-Heap’ для исследования быстродействия s-арных пирамидальных сортировок. В эксперименте s-сортировкам подвергались массивы разной длины, состоящие из псевдослучайных целых чисел разных диапазонов значений. Просчет был реализован на персональном компьютере IBM PC c процессором Pentium-166 и ОЗУ - 64 Мб. При этом получены следующие выводы:
|
S-арные пирамидальные сортировки при любом фиксированном s (s = 2, 3, …) могут быть организованы на месте расположения массива без дополнительной памяти и с гарантированным порядком трудоемкости, равным (s + 1)×(n - 1)×logs(n×(s - 1)) операций сравнения и перемещения (см. главный член в оценке леммы 3). |
|
В достаточно широком диапазоне длин массивов оптимальное значение величины s лежит в диапазоне 6..9 и, как правило, равно 7. Поневоле задумаешься о считающемся сакральным и в науке, и в искусстве, и в религии числе 7, простирающем свои мистические щупальца к цветам радуги, нотам музыкальной гаммы, дням недели, чудесам света, античным мудрецам, смертным грехам… . | |
|
Выигрыш во времени при сортировке 7-арными пирамидами по сравнению с бинарными сортировками достигает 30-35 процентов. |
Остается доказать три леммы, на утверждения которых мы ссылались выше. Напомним, что высотой s-арного дерева называется величина, равная количеству его уровней без единицы, а узлы дерева и его уровни пронумерованы целыми неотрицательными числами от нуля и далее.
Лемма 1. В s-арном дереве (s = 2, 3, …) с n вершинами наименьший номер p вершины, не имеющей потомков, вычисляется по формулам:
Доказательство. При n=1 утверждение леммы очевидно. Пусть n>1. Потомками вершины-родителя x являются вершины с номерами x×s+1, x×s+2, …, x×s+s (может быть, не все). Номер последней вершины последнего уровня дерева равен n-1. Если x - номер родителя для вершины n-1, то существует j такое, что
![]()
Тогда
![]()
Следовательно,
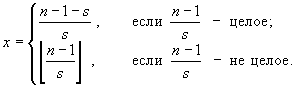
Номер p первой из вершин, не имеющих потомков, очевидно, равен x+1. Иными словами
Отсюда и вытекает первая из формул (28).
Доказательство справедливости второй из этих формул можно провести так. Пусть n = m×s + r (0 £ r £ s-1). Рассмотрим два случая.
A. При r = 0 или r = 1 имеем:
![]()
![]()
B. При 2 £ r £ s-1 имеем:
![]()
![]()
Тем самым лемма 1 доказана полностью.
Следствие 1. При s=2 из (28) получаем:Следствие
2. При s=3 из
(28) получаем: ![]()
Лемма 2. Высота k = k(n, s) s-арного дерева (s=2, 3, …) с n узлами определяется по формулам:
k(n, s) = élogs(n×(s - 1) + 1)ù - 1, (29)
k(n, s) = ëlogs((n - 1)×(s - 1) + 1)û. (30)
Доказательство. Организуем подсчет величины k(n, s) двумя способами, которые и установят соотношения (29) и (30). Способ 1. Пусть j и k - номера соответственно произвольного и последнего уровней дерева. При j<k на уровне j находится ровно sj узлов. На уровне k их может быть любое количество от 1 и до sk включительно. Тогда n - общее число узлов дерева - должно удовлетворять условиям:
![]()
Отсюда последовательно получаем:
![]()
Следовательно, для k имеем неравенства:
logs(n×(s - 1) + 1) - 1 £ k < logs(n×(s - 1) + 1).
Если a = logs(n×(s - 1) + 1), то a - 1 £ k < a. Иными словами, k - наименьшее целое, большее или равное a - 1: k = éa - 1ù = éaù - 1. Тем самым (29) установлено.
Способ 2. Пусть на уровне p-1 (p=1, 2, ...) первый, то есть самый левый, узел имеет номер dp-1. Тогда ясно, что на уровне p первая вершина dp будет иметь номер dp-1 + sp-1. Иными словами, относительно dp имеет место следующая, легко разрешаемая рекуppентность:
Отсюда имеем:
![]()
Из последнего соотношения следует, что для каждого узла с номером x на уровне p справедливы неравенства:
p £ logs(x×(s - 1) + 1) < logs(dp+1×(s - 1) + 1) = p + 1,
то есть
p = ëlogs(x×(s - 1) + 1)û.Отсюда при p=k и x=n-1, где k и n - соответственно номера последнего уровня дерева и количество его узлов, получаем (30).
Следствие 1. При целых s³2 и n³1 имеет место равенство:élogs(n×(s - 1) + 1)ù = ëlogs((n - 1)×(s - 1) + 1)û + 1 (31)
и, в частности, при s=2 имеем:
élog2(n + 1)ù = ëlog2(n)û + 1 (32)
Соотношения (31) и (32) вытекают из равенства левых частей в (29) и (30). Впрочем, (32) несложно доказать и непосредственно, рассматривая его справедливость на последовательных непересекающихся участках nÎ[2k, 2k+1-1] (k = 0, 1, ...).
Следствие 2. Высота бинарного дерева равна ëlog2(n)û.Следствие 3. Высота тернарного дерева равна ëlog3(2×n-1)û.
Следствие 4. Имеет место следующее соотношение:
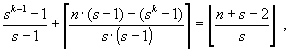 (33)
(33)
где k - высота s-арного дерева с n вершинами (см. формулы (29) и (30)).
Доказательство этого равенства можно провести так. На последнем уровне дерева находится n-(sk-1)/(s-1) вершин. Следовательно, на предпоследнем уровне количество вершин, имеющих потомков и не имеющих потомков, равно соответственно:
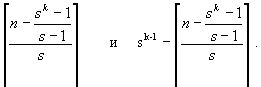
Тогда общее количество вершин, не имеющих потомков, равно:
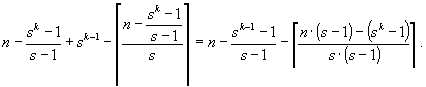
Следовательно, наименьший номер p вершины без потомков может быть вычислен так:
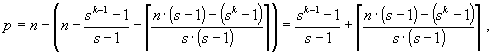
что вместе с (28) и доказывает справедливость (33).
Лемма 3. Описанный ранее алгоритм сортировки s-арными пирамидами (см. этапы: построение s-пирамиды, сортировка s-пирамиды) реализуется не более чем за![]() (34)
(34)
операций сравнения и перемещения (обмена).
Доказательство. Пусть k - высота s-арного дерева для сортируемого массива (17). Из утверждения леммы 2 следует, что k = ëlogs((n - 1)×(s - 1) + 1)û. Оценим сверху общее количество операций сравнения и перемещения, необходимых для s-сортировки (17).A. Для просеивания конкретного элемента массива на один шаг вниз по дереву требуется выполнить не более s операций сравнения и одной операции перемещения, то есть общее число операций равно s+1.
B.
Оценим сверху количество шагов b1, необходимых для просеивания элементов
вниз по дереву на первом этапе s-сортировки,
то есть при построении пирамиды. Рассмотрим
таблицу 2. В ней указано количество
элементов, просеиваемых вниз на каждом
уровне, и верхняя граница количества
совершаемых при этом шагов. Пояснений, по-видимому,
требует лишь последняя строка таблицы.
Наименьший номер p из вершин, не имеющих
потомков, равен
ë(n+s-2)/sû.
Первая вершина k-1 уровня
имеет номер (sk-1-1)/(s-1).
Следовательно, количество вершин k-1 уровня, обладающих потомками, равно:
![]()
Таблица 2
|
№ уровня |
Количество элементов |
Количество шагов перемещения вниз по дереву |
|
0 |
Один элемент из корня |
Не более чем на k шагов |
|
1 |
S элементов первого уровня |
Не более чем на k-1 шагов |
|
… |
… … … |
… … … |
|
k-2 |
sk-2 элементов (k-2)-го уровня |
Не более чем на 2 шага |
|
k-1 |
|
Не более чем на 1 шаг |
Таким образом, для b1 получаем такую оценку сверху:
![]() (35)
(35)
C. Теперь оценим сверху общее количество шагов b2, необходимое для просеивания элементов вниз по дереву, начиная от корня, на втором этапе s-сортировки. Исходя из информации, представленной в таблице 3, получаем:
 (36)
(36)
|
№ |
Количество элементов |
Количество шагов перемещения вниз по дереву |
|
0 |
|
Не более чем на k шагов |
|
1 |
Один элемент k-го уровня и sk-1-1 элементов (k-1)-го уровня, помещенных в корень дерева. Всего sk-1 элемент |
Не более чем на k-1 шагов |
|
… |
… … … |
… … … |
|
k-1 |
Один элемент 3-го уровня и s2-1 элементов 2-го уровня, помещенных в корень дерева. Всего s2 элементов |
Не более чем на 2 шага |
|
k |
Один элемент 2-го уровня и s-1 элементов 1-го уровня, помещенных в корень дерева. Всего s элементов |
Не более чем на 1 шаг |
Кроме того, на этом этапе проводится (n-1) дополнительных перемещений элементов из корня дерева в конец еще не отсортированной части массива.
D. Теперь можно оценить общее количество l = l(n, s) операций сравнения и перемещения при s-сортировке массива длины n. Из (35), (36) и последнего замечания предыдущего пункта имеем:
![]()
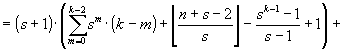
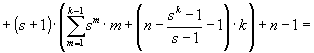
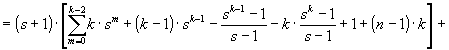
![]()
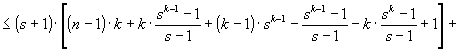
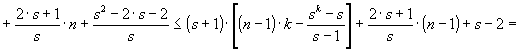
![]()
![]()
![]()
![]()
Тем самым утверждение леммы 3 доказано полностью.
![]()