Рассмотрим две задачи, относящиеся к возвратным уравнениям. Начнем с определения.
Уравнение вида
a0×xn + a1×xn-1 + ... + an = 0 (20)
называется возвратным (или возвратным первого рода), если a0 ¹ 0 и коэффициенты членов левой части (20), равноотстоящие от концов, равны между собой. Левую часть (20) называют возвратным многочленом. Записать его можно так:
f(x) = a0×xn + a1×xn-1 + ... + a1×x + a0 .
В дальнейшем нам будут полезны следующие простейшие свойства возвратных уравнений.
 | Возвратное уравнение не имеет корней, равных нулю (a0 ¹ 0). |
| Если b есть корень (20), то 1/b также является корнем (20). В самом деле: |
| Возвратное уравнение f(x)=0 нечетной степени всегда имеет корень, равный -1: |
f(-1) = -a0 + a1 - a2 + ... + a2 - a1 + a0 = 0.
| Частное от деления многочлена f(x) нечетной степени на x+1 снова является возвратным многочленом (доказывается по индукции). |
Последнее свойство сводит вопрос о решении любых возвратных уравнений к решению возвратных уравнений лишь четной степени:
a0×x2×n + a1×x2×n-1 + ... + ak×xk + ... + a1×x + a0 = 0. (21)
Но для (21) можно записать равносильное уравнение:
(22)
Далее, если положить y=x+1/x и учесть “символьную рекуррентность”:
(23)
то индукцией по n доказывается, что левая часть (20) выражается через y в виде некоторого многочлена jn(y) степени n.
адача
47. Пусть
Написать рекурсивную программу-функцию, возвращающую вектор последовательных коэффициентов многочлена jn(y) от старшей степени и ниже.
Решение. Из определения jn(y) и соотношений (23) вытекает, что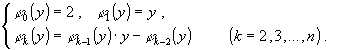 
(24)
Обозначим через a(k) (k=0, 1, …, n) векторы коэффициентов многочленов jk(y) и дополним их до длины n+1 начальными нулевыми компонентами. Тогда
a(0) = (0, 0, ..., 0, 2)T и a(1) = (0, 0, ..., 1, 0)T.
Далее, если уже определены векторы a(k-2) и a(k-1), то в соответствии со второй строкой (21) a(k) можно построить следующим образом. Начальную компоненту a(k-1) удаляем, к концу усеченного вектора добавляем нулевую компоненту и из результата вычитаем вектор a(k-2) .
Именно эти идеи и реализованы в рекурсивной функции coeff(n,v,w,k), куда в качестве фактических параметров из головной программы coef(n) передаются значения n, v=a(0), w=a(1), а также вспомогательный параметр k, имеющий начальное значение, равное n, и служащий для организации рекурсивных обращений.
Контрольные примеры:
coef(1)T = [1 0], coef(4)T = [1 0 -4 0 2],
coef(9)T = [1 0 -9 0 27 0 -30 0 9 0].
адача
48.
Написать рекурсивную программу-функцию,
сводящую возвратное уравнение (21) степени 2×n
(n=1, 2, …) к уравнению j(y)=0 степени n
относительно переменной y=x+1/x.
Результат должен быть возвращен в виде
вектора последовательных коэффициентов j(y), начиная со старшей
степени и далее.
При обращении к функции equa(A) в качестве фактического параметра должен передаваться вектор с компонентами, представляющими собой первые n+1 последовательных коэффициентов исходного возвратного уравнения.
Контрольный пример:
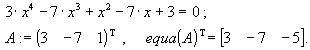
Иными
словами, получили уравнение: 
Замечание. Уравнение f(x)=0 называют возвратным уравнением второго рода, если многочлен f(x) имеет четную степень и его коэффициенты, равноотстоящие от концов, при четных степенях x равны, а при нечетных - равны по абсолютной величине и противоположны по знаку. Для таких уравнений степень также может быть понижена в два раза. Делается это подстановкой z=x-1/x.
