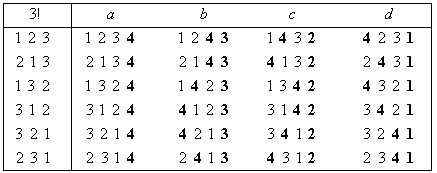
При S={1} имеем одну перестановку - 1. Если уже имеется последовательность перестановок из n-1 элемента {1,2,…,n-1}, то получить все перестановки из n элементов {1,2,…n} можно способом, который мы будем именовать как “метод последовательного замещения” элемента n. Суть его в следующем. Рассмотрим n идентичных экземпляров (групп) последовательностей перестановок из элементов {1,2,…,n-1}. В первом экземпляре, как и в методе вертикальной прогонки, в конец каждой перестановки поместим элемент n. В каждой перестановке второго экземпляра поменяем местами элементы n и n-1. В каждой перестановке третьего экземпляра поменяем местами элементы n и n-2 и т. д. Наконец, в последнем экземпляре поменяем местами элементы n и 1. На рис. 2 описанная процедура демонстрируется при переходе от n=3 к n=4. Нетрудно понять, что указанные действия любую перестановку из n- 1 элемента переводят в некоторую перестановку из n элементов. При этом общее количество полученных перестановок равно n!. Остается показать, что среди них нет совпадающих. Если взять две сгенерированные перестановки внутри одной группы, то они обязательно будут отличаться друг от друга расположением элементов на позициях от 1 до n-1 и, значит, не могут быть совпадающими. Если же взять перестановки из разных групп, то на последних позициях у них стоят разные элементы и перестановки опять не могут быть совпадающими. Таким образом, все полученные n! перестановок различны.

Рис. 2. Генерирование перестановок последовательным замещением

адача 2. Написать рекурсивную программу-функцию генерирования всех перестановок из n элементов 1,2,…,n методом последовательного замещения.

Решение. Описанный выше алгоритм последовательного замещения реализуется рекурсивной программой-функцией permut2(n):

                      (2)