адача 1. Странное число 153. Первый член последовательности равен любому натуральному числу n, кратному 3, а каждый последующий член равен сумме кубов цифр её предыдущего члена. Доказать, что члены любой такой последовательности начиная с некоторого места равны 153 [11, c.30].

Решение. Пусть sumcub(n) есть сумма кубов десятичных цифр натурального числа n. Нам требуется установить, что для любого n, кратного 3, после конечного числа рекурсивных шагов вида n¬sumcub(n) получится число 153. Просчет нескольких примеров позволяет надеяться, что утверждение теоремы, по-видимому, имеет место:

A. n = 3,             3® 27® 351® 153;

B. n = 477,         477® 750® 468® 792® 1080® 513® 153;

C. n = 41121,     41121® 75® 468® 792® 1080® 513® 153;

D. n = 77106,     77106® 903® 756® 684® 792® 1080® 513® 153.

1. При рассмотрении многозначных чисел с количеством цифр более четырех бросается в глаза, что второй член последовательности меньше первого (см. два последних примера). Возможно, это общий факт? Оказывается, да:

“Если n>9999, то sumcub(n)<n.”                                                  (1)

Установить справедливость (1) можно так. Пусть число n>9999 и содержит k цифр. Тогда имеют место соотношения

sumcub(n) ³ k × 9³ = 729 × k,           10^k-1 £ n < 10^k.                                  (2)

Но из n>9999 следует, что k³5 и, следовательно, 729 × k < 10^k-1. Этот факт вместе с (2) и доказывает (1). Иными словами, члены рассматриваемых последовательностей убывают, по крайней мере, до того места, пока не становятся меньше 10000.

2. Нам потребуется также доказать, что все члены любой последовательности, формируемой по условиям задачи, кратны 3, то есть

                                                        (3)

Докажем (3). Пусть . Тогда

Следовательно:

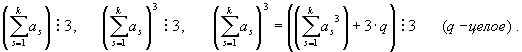
Последнее из этих соотношений и доказывает (3).

3. Что же нам еще осталось сделать? Если бы удалось установить, что для всех n кратных 3 и меньших 10000, утверждение задачи 51 верно, то из предыдущих рассуждений следовало бы, что оно верно для любого n. В самом деле, отправляясь от произвольного n, кратного 3 и не меньшего 10000, за конечное число шагов мы получим член последовательности , опять кратный 3 и уже меньший 10000. Следовательно, для этого n утверждение задачи верно.

Теперь к делу может приступить компьютер. Конечно, еще необходимо составить программу, по которой он будет последовательно для каждого n, кратного 3 и меньшего 10000, проверять справедливость утверждения задачи. Но это уже несложная проблема. Ниже приведены рекурсивные программы-функции sumcub(), ite() и программа-константа theorem, которые, реализуя указанные действия, завершают доказательство нашей теоремы.

Кратко опишем эти программы.

Функция sumcub(n) по натуральному числу n, кратному 3, находит и возвращает число, равное сумме кубов цифр n. Как мы уже видели раньше, это полученное число снова натуральное и кратно 3. Декомпозиция задачи организована по цифрам n, начиная с младшего разряда и далее. Базой рекурсии являются однозначные числа. Количество рекурсивных вызовов равно разрядности n.

Функция ite(n) рекурсивным образом итерирует действия, реализуемые функцией sumcub(n). Базой рекурсии выбрано значение n=153. Количество рекурсивных вызовов зависит от начального значения n. Если доказываемое нами утверждение справедливо, то ite(n) для любого n<10000 достаточно быстро должна заканчивать свою работу, возвращая 153. В противном случае для некоторого n она не сможет завершить вычисления нормально (не аварийно). Последняя ситуация гипотетически возможна лишь тогда, когда на некотором рекурсивном шаге sumcub(n) окажется равным уже ранее встречавшемуся значению в последовательности генерируемых чисел. Учитывая сказанное, функцию ite() можно было бы написать более “грамотно” так, чтобы отлавливались все случаи периодичности формируемой последовательности, если вдруг такое обнаруживается. Но мы этого делать не будем.

Программа theorem запускает последовательные вычисления по ite(n) для всех n от 3 до 9999 с шагом 3. Нормальное завершение вычислений по theorem будет означать справедливость утверждения задачи 51.

Контрольные вычисления:

theorem = 153 - это означает, что утверждение задачи 51 доказано.

Замечание. В связи с задачей 1 интересными могут оказаться некоторые вспомогательные подзадачи. Сформулируем две из них и приведем программы их решения:

Решение может быть получено с помощью рекурсивной функции len(n, k) и программы-константы lenmax. Первая из них для данного n находит и возвращает длину k начальной части последовательности до члена 153. Обращение к этой функции должно выглядеть так: len(n,0). Вторая программа решает поставленную задачу, многократно обращаясь к len(n,k) со значениями от 3 до 9999 с шагом 3. В процессе вычислений в виде компонентов вектора запоминается первое из значений n c наибольшим на текущий момент предпериодом последовательности и длина этого предпериода. Ниже, справа от lenmax, приведен результат счета по этой программе:

Число 177 не единственное из диапазона 1..10000, для которого соответствующая последовательность имеет наибольший предпериод (длиной 13). Если бы, например, мы искали не наименьшее, а наибольшее n с этим же свойством, то получили бы n=9774. Для организации такого поиска потребовалось бы в четвертой строке lеnmax знак “<” заменить на знак “£ ”.

Решение может быть получено с помощью рекурсивной функции begin(n), по которой в виде компонентов вектора запоминается число n и все последовательно получаемые по sumcub() числа до 153 включительно:

Ранее мы установили (см. пример для lenmax), что одна из последовательностей с наиболее длинным периодом начинается с числа 177. Поэтому сам предпериод (вместе с числом 153) можно получить так:

Заметим, что в диапазоне 1..10000 имеется ровно 48 чисел, для которых длина предпериода последовательности равна 13 и, что весьма любопытно, каждое из них в своей десятичной записи имеет цифру 7, а все предпериоды имеют общую “хвостовую” часть вида: 99, 1458, 702, 351.