
Пусть, как и ранее, A - невырожденная матрица размером n´n и E - единичная матрица того же размера. Тогда существует и единственна обратная матрица A-1 - такая, что A × A-1 = A-1 × A = E. Находить её можно по-разному, что и отражается постановкой задач 4-6.
![]() адача
4. LU-обращение
матриц. Составить рекурсивную программу-функцию
нахождения обратной матрицы, используя LU-разложение
исходной квадратной невырожденной матрицы A
размером n´n.
адача
4. LU-обращение
матриц. Составить рекурсивную программу-функцию
нахождения обратной матрицы, используя LU-разложение
исходной квадратной невырожденной матрицы A
размером n´n.
A × x = b (b Î {e0, e1, ..., en-1}), (17)
где все компоненты каждого вектора ek (k = 0 .. n-1) равны нулю, кроме компоненты с индексом k, равной единице. Последнее обстоятельство непосредственно вытекает из определения обратной матрицы: A × A-1=E. С помощью LU- или LUP-разложения каждая такая система, как мы уже видели, решается с трудоемкостью Q(n2) операций. Поэтому решение всех систем (17) может быть реализовано за Q(n3) операций.
На основе LU-разложения A получить обратную для неё матрицу можно с помощью функции invers1(A), обращающейся к рекурсивной функции inve1(M,n,k). В качестве фактических параметров в inve1() передаётся: вектор с компонентами LU-разложения A, а также конечное (n-1) и начальное (0) значения номеров решаемых систем (17). В каждом рекурсивном вызове inve1() формируется очередной свободный член ek (k = 0 .. n-1) и решается соответствующая ему система. Результаты вычислений отдельных вызовов запоминаются в виде столбцов возвращаемой обратной матрицы:
![]() адача
5. LUP-обращение
матриц. Составить рекурсивную программу-функцию нахождения
обратной матрицы, используя LUP-разложе-ние
исходной квадратной невырожденной матрицы A
размером n´n.
адача
5. LUP-обращение
матриц. Составить рекурсивную программу-функцию нахождения
обратной матрицы, используя LUP-разложе-ние
исходной квадратной невырожденной матрицы A
размером n´n.
Заметим, что в рекурсивной функции inve2() при решении очередной k-й системы свободный член формируется как столбец с индексом k матрицы перестановки P = M2.
Контрольный пример.
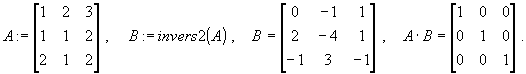
![]() адача
6. Обращение
матриц разбиением на клетки. Составить
рекурсивную программу-функцию нахождения
обратной матрицы, используя разбиение
исходной квадратной невырожденной матрицы S
размера n´n
на клетки.
адача
6. Обращение
матриц разбиением на клетки. Составить
рекурсивную программу-функцию нахождения
обратной матрицы, используя разбиение
исходной квадратной невырожденной матрицы S
размера n´n
на клетки.
![]() (22)
(22)
где квадратные диагональные матрицы A и D имеют соответственно порядки p и q (p+q=n). Положим,
W = D-1, K = (A - B × W × C)-1, L = -K × B × W, M = -W × C × K, N = W - W × C × L. (23)
Если матрицы W и K существуют, то нетрудно проверить, что размеры пар A и K, B и L, C и M, а также D и N совпадают и
![]() (24)
(24)
Вычисления элементов матрицы (24) можно организовать более эффективно, проводя их в последовательности:
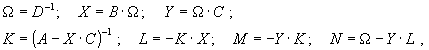 (25)
(25)
Беря формулы (25) в качестве расчетных для нахождения S-1 и считая порядки диагональных матриц приближенно равными n/2, нам придется совершить два обращения и шесть умножений таких матриц. Так часто и поступают. Но можно пойти дальше, рассматривая формулы (25) как декомпозиционные, рекурсивно применяя их к вычислению обратных матриц, полученных на первом этапе, и т. д., а в качестве базы рекурсии взять случай, когда порядок вычисляемой обратной матрицы становится равным единице. Именно эти соображения и реализуются рекурсивной функцией inve3(S):
Из проведенных рассуждений вытекает, что вычисления по формулам (25), а значит и с помощью функции inve3(S), не всегда возможны. Однако если S - симметрическая положительно-определенная матрица, то этим же свойством обладают матрицы D и A - B × D-1 × C. Следовательно, они обратимы [36, с. 688- 704] и потому по формулам (25) матрица S-1 может быть найдена. Этот факт с успехом используется для обращения произвольной невырожденной матрицы S. Дело в том, что S-1 = (ST × S)-1× ST, а ST × S - симметрическая положительно-определенная матрица. Отсюда S-1 можно находить с помощью ранее построенной функции inve3(S) следующим образом:
Замечание. Для симметрических положительно-определенных матриц S можно записать более эффективный аналог функции inve3(S), сократив требуемое количество умножений матриц с шести до четырех. Соответствующая рекурсивная функция inve4(S), приведенная ниже, базируется на возможности представления обратной для S матрицы в следующем клеточном виде [36, с. 702]:
W = (D - C × A-1 × B)-1,

Ничто не мешает использовать inve4(S) и для обращения произвольных квадратных невырожденных матриц S. Делать это можно, например, с помощью функции
При этом нелишне помнить, что из-за ошибок округления вычисления по invers4(S) могут “привести к успеху” и при вырожденной матрице S. Следовательно, если заранее об S ничего не известно, то полученный результат обязательно следует подвергать той или иной проверке на достоверность.
Контрольный пример.
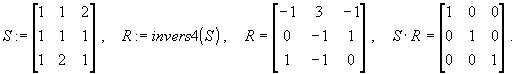
![]()