Ниже приведен рекурсивный способ разложения квадратной невырожденной матрицы A в произведение нижней треугольной L и верхней треугольной U матриц одного с A размера, причем каждый элемент главной диагонали L равен единице. Этот способ есть не что иное, как широко известный метод Гаусса исключения неизвестных. Он не всегда приводит к цели. Для успешной реализации метода требуется, чтобы элементы главной диагонали A в процессе вычислений не обращались в нуль. Эти элементы называют ведущими.

Представление матрицы A в виде A = L×U называют её LU-разложением. Суть его в следующем. Если A=(A_i,j) (i, j = 0 .. n-1) представить в клеточном виде как

                                                              (1)

то простым умножением можно проверить правильность разложения:

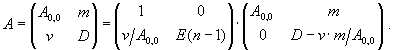                         (2)

Нули в первой и второй матрицах правой части этого равенства обозначают нулевые клетки размеров соответственно 1´(n-1) и (n-1)´1, а E(n-1) - единичную матрицу размера (n-1)´(n-1). Разность

W = D - v × m / A_0,0 ,                                                   (3)

существующая лишь при A_0,0 ¹ 0, называется дополнением Шура. Рекурсивно применяя к (3) соотношение (2), получим для него LU-разложение: W = L1×U1. Это позволяет получить LU-разложения для исходной матрицы:

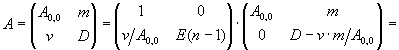
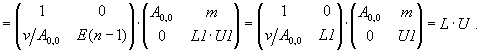              (4)

Теперь можно перейти к составлению рекурсивной программы-функции, реализующей LU-разложение.

адача 1. LU-разложение. Составить рекурсивную программу-функцию, находящую методом Гаусса LU-разложение для невырожденных квадратных матриц A размером n´n. При неудаче функция должна возвращать пользовательское сообщение об ошибке.

Решение. В качестве базы рекурсии может быть взят случай n=0, при котором задача решается очевидным способом: L=id, U=A_0,0×id. Далее, соотношения (2)-(4) задают правило декомпозиции. Рекурсивная функция LU(A) полностью построена именно на этих соображениях. Результат вычислений, если это не сообщение об ошибке, выводится в виде составного массива - вектора c матричными компонентами L и U:

                             (5)

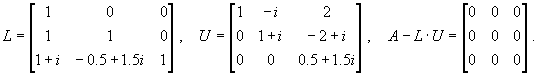
Несколько слов о трудоемкости задачи. Оценим количество арифметических операций при вычислениях по функции LU(A). В каждом из (n-1)-го рекурсивных вызовов формируется аргумент для LU(), а его вычисление в виде дополнения Шура реализуется за Q(n²) операций. Поэтому общее количество требуемых операций имеет порядок Q(n³).

Замечание. При необходимости построенную рекурсивную функцию LU(A) можно преобразовать в её нерекурсивный аналог. Используя дополнительные приемы оптимизации, не будем заводить вспомогательные переменные и результирующие матрицы L и U, а сформируем значащие элементы последних в соответствующих местах A: L (без диагональных единиц) - в “нижнем левом” треугольнике A, U - в “верхнем правом” треугольнике A. Сделать это можно, например, по такой изящной программе-функции:
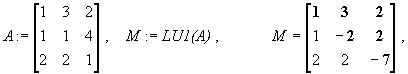
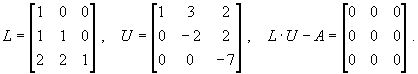