Для вычисления функции dns() предыдущего пункта требовалось находить значение целой части корня квадратного из натурального числа. Подобная необходимость возникает и во многих иных случаях. Опишем, как это можно делать, оперируя лишь целыми неотрицательными числами.

адача 22. Целая часть корня квадратного. Составить рекурсивную функцию вычисления целой части от арифметического значения корня квадратного из натурального числа, оперируя лишь с целыми неотрицательными числами.

Решение. Заметим, что для целой части m ниже используется стандартное обозначение [m]. Построить требуемую рекурсивную функцию можно, исходя из такого представления целой части корня квадратного:

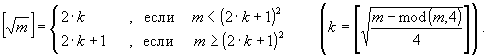                          (7)

Эта формула определяет рекурсию c декомпозицией от значения m к значению k. Доказательство справедливости (7) вытекает из более общего представления (10), которое далее подробно обосновывается. Соответствующая рекурсивная функция sq(m) решения исходной задачи могла бы выглядеть так:

                                                          (8)

 Трудоемкость вычислений по sq(m), как и глубина рекурсивных вызовов, составляет O(log₄(m)) арифметических операций.

Контрольные примеры:

адача 23. Целая часть корня p-й степени. Составить рекурсивную функцию вычисления целой части от арифметического значения корня p-й степени (p=2,3,…,) из натурального числа, оперируя лишь с целыми неотрицательными числами.

Решение. Вид искомой функции sqp(m) нетрудно предугадать, исходя из (8):

                                                   (9)

 Займемся обоснованием нашей догадки. Обсудим алгоритм, положенный в основу построения sqp(m). Прежде всего, заметим, что для любого натурального m найдется единственное k такое, что

2^p× k^p £ m < 2p× (k+1)^p+1 .

В самом деле, m = 2^p× q + r (0 £ r < 2^p ) при некоторых целых неотрицательных q и r. Тогда:

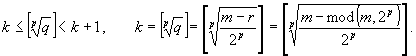
Далее, , то есть может принимать лишь два значения 2× k и 2× k+1. Точнее,

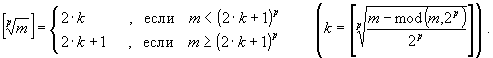                   (10)

 Эта формула определяет рекурсию c декомпозицией от значения m к значению k, которая один к одному реализуется функцией sqp(m). Заметим, что здесь мы, благодаря рекурсии, имеем тот самый не столь частый случай, когда удается четко провести доказательство правильности программы.

Трудоемкость вычислений по sqp(m), как и глубина рекурсивных вызовов, составляет O((1/p)× log₂(m)) арифметических операций. Соотношения (7) предыдущей задачи получаются из (10) при p=2.

 Контрольные примеры:

Замечание. Формула (10) имеет место при любом вещественном m³0 и натуральном p (p=2,3,…,). Это вытекает из равенства , справедливость которого подтверждается приведенной ниже цепочкой соотношений. Пусть . Тогда:

Тем самым, рекурсивную функцию (9) можно использовать для вычисления целой части от арифметического значения корня p-й степени из любого вещественного числа m³0.