
Рекурсия называется удаленной, если в теле функции при рекурсивных вызовах, в выражениях, являющихся фактическими параметрами, снова встречаются рекурсивные вызовы этой функции. Подобный пример дает нам классическая в теории рекурсии функция Аккермана:
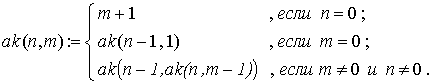
Вычислить её непосредственно исходя из определения удается лишь для некоторых малых значений n и m. Связано это со сложностью и необычностью удаленной рекурсии. В общем случае не только ak() вычисляется через ak(), но и второй из аргументов функции также требует рекурсивного вызова ak(). Соответствующая программа-функция может быть записана так:
Контрольные примеры:
![]()
Следующий вариант программы для вычисления функции Аккермана включает в себя лишь один рекурсивный вызов:
Замечание. Для m=0..4 справедливы соотношения [15, с. 69]:
ak(0, n) = n+1; ak(1, n) = n+2; ak(2, n) = 2×n+3; ak(3, n) = 2n+3- 3;
ak(4, n) = 2s(n)-3 [s(0) = 22, s(n+1) = 2s(n) (n=0, 1, …)].
Эти формулы могут оказаться полезными при построении контрольных примеров для отладки новых, более эффективных вариантов программ вычисления функции Аккермана.
Удаленная рекурсия не обязательно приводит к громоздким вычислениям. Например, если sum(n) - сумма цифр целого неотрицательного числа n и итерированную сумму qsum(n) определить равной значению первого из элементов числовой последовательности np=sum(np-1) (n0=n; p=1, 2, …), меньшего десяти, то находить qsum(n) можно с помощью следующей удаленной рекурсии [Бр, с.154]:
Заметим, что если k - количество десятичных цифр числа n, то для вычисления qsum(n) требуется не более 2×k рекурсивных вызовов. Впрочем, вычисление qsum(n) можно было бы организовать и с помощью простой повторительной рекурсии:
![]()