адача 39. Вложенные квадраты. Пусть на плоскости первый квадрат задан точками:  M₁(-1,-1), M₂(-1,1), M₃(1,1), M₄(1,-1). Второй квадрат строится так, что вершины первого квадрата являются серединами его сторон и т. д. Составить рекурсивную программу-функцию, которая по заданному натуральному числу n строит систему из 2×n вложенных друг в друга описанным образом квадратов, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис.7).

Решение. Если учесть тот факт, что по условию задачи всегда строится четное число вложенных квадратов, то последовательность точек для построения первых двух из них можно задать непосредственно и считать соответствующую матрицу beg базой рекурсии:

Обратите внимание, что в beg каждый из квадратов задается не четырьмя, а пятью точками. При этом первая и последняя из них совпадают. Это поможет впоследствии правильной прорисовке квадратов.

Далее, декомпозиция определяется таким утверждением. Если уже построена матрица ma точек для 2×(n-1) вложенных квадратов, то, пополнив её точками матрицы 2^n-1×beg, получим матрицу точек для 2×n таких квадратов. Соответствующая рекурсивная функция, базирующаяся на этих фактах, может выглядеть так:

Контрольный пример: z := squ(4),    x := z^<0>,    y := z^<1>.

Результат вычислений представлен на рисунке 7 c неодинаковым масштабом по осям.

Рис. 7. Вложенные друг в друга 2×n квадратов (n=4)

адача 40. Вложенные многоугольники. Пусть на плоскости задан правильный n-угольник, вписанный в единичную окружность, одна из вершин которого имеет координаты (cos(a ), sin(a )), где a - некоторый угол. Второй правильный n-угольник строится так, что его вершины являются серединами сторон первого многоугольника и т. д. Составить рекурсивную программу-функцию, которая по заданному натуральному числу n строит систему из n вложенных друг в друга описанным образом многоугольников, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис.8).

Решение. Это задача в каком-то смысле является обобщением предыдущей. Здесь выводятся правильные вписанные n-угольники, количество их не обязательно четно и первая из вершин начального n-угольника может лежать в любой точке единичной окружности. Правда, здесь многоугольники не “описываются” один вокруг другого, а “вписываются” друг в друга. Но существа дела это не меняет.

Прежде всего, составим программу, которая формирует массив вершин правильного n-угольника, вписанного в окружность радиуса r и содержащего вершину (r×cos(a) r×sin(a)). Сделать это можно, например, так:

Тогда массив polyone(n,1,a ) может служить базой рекурсии. Более того, эта функция при правильном выборе r и a позволяет получить массив вершин любого из следующих вписанных n-угольников, что помогает организовать и декомпозицию. Если уже построена матрица ma точек для (n-1)-го вписанного правильного n-угольника, то, пополнив её точками матрицы:

получим матрицу точек для 2×n таких многоугольников. Соответствующая рекурсивная функция, реализующая эти идеи, может выглядеть так:

Контрольный пример:  u := polygons(20, 6, p/18),    x := u^<0>,    y := u^<1>.

Результат вычислений представлен на рисунке 8 c неодинаковым масштабом по осям.

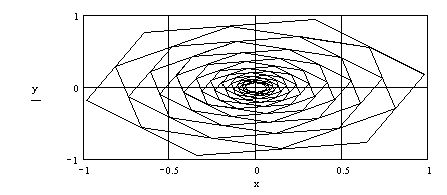
Рис. 8. k вложенных правильных n-угольников (k=20, n=6)