Бинарная пирамидальная сортировка

Все методы сортировок основаны на многократных просмотрах массивов v и выполнении определенных операций над их элементами. Как можно улучшить какой-либо из конкретных алгоритмов? По-видимому, путь таков: за каждый просмотр всего v или его части получать как можно больше информации. Одна из возможностей на этом пути открывается при представлении сортируемого массива в виде нелинейной структуры типа двоичного (бинарного) дерева D. На рис.1 показан такой граф D для v из n элементов, где 8 £ n < 16.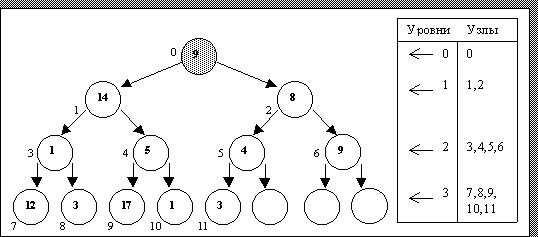

Рис. 1. Бинарное дерево последовательности (7)

В кружках-вершинах графа размещены элементы массива:

9, 14, 8, 1, 5, 4, 9, 12, 3, 17, 1, 3. (7)

Целыми последовательными числами, начиная от 0 и далее, сверху вниз по уровням и слева направо на одном уровне пронумерованы все узлы, или вершины, D. Эти номера (адреса, индексы) проставлены около узлов. Именно такая адресация и будет использоваться в дальнейшем. У любого бинарного дерева имеется, и притом только один, корневой узел (корень), для которого нет предшественников (родителей). Любой другой узел имеет только одного предшественника и одного или двух преемников (прямых потомков). Высотой бинарного дерева называют число, равное количеству уровней расположения его узлов без единицы.

Ниже используются следующие стандартные для информатики обозначения: éxù - “потолок” x, функция, определяемая как наименьшее целое, большее или равное x; ëxû - “пол” x, функция определяемая как наибольшее целое, меньшее или равное x (то есть ëxû = floor(x) = [x]).

Нетрудно видеть, что в бинарном дереве с n вершинами высота равна floor(log₂(n))=ëlog₂(n)û (см. лемму 2 при s=2).

На представлении массивов в виде двоичных деревьев основана большая серия так называемых древовидных или турнирных сортировок. Друг от друга они отличаются способом представления исходной и сопутствующей информации, объемом дополнительно используемой памяти и т.п. Об одном из таких алгоритмов, предложенном Дж.Уильямсом и развитом Р.Флойдом, и пойдет речь ниже [3; c.6]. Называется он пирамидальным, для реализации не требует дополнительной памяти и имеет трудоемкость O(n×log₂(n)).

Начнем с определения пирамиды - некоторой структуры для представления данных с отношением порядка. В нашем случае данные являются целыми или действительными числами. Пусть задан массив:

v₀, v₁, ... , v_n_-1. (8)

Бинарной пирамидой, или просто пирамидой, массива (8) называется непустая подпоследовательность его элементов вида

v_p, v_p+1, ... , v_q (0 £ p £ q £ n-1), (9)

для которой выполнено одно из следующих условий:

1. 2 × p + 1 > q;

2. 2 × p + 1 £ q и v_j ³ v₂_×_j+1 для p £ j £ (q-1)/2,

v_j ³ v₂_×_j+2 для p £ j £ (q-2)/2.

Из этого определения вытекают такие утверждения:

Для всякой последовательности (8) любой фрагмент её “хвостовой части”, то есть подпоследовательность

v_p, v_p+1, ... , v_n-₁ ( p ³ ën/2û), (10)

является пирамидой. Если (8) представлена в виде бинарного дерева, то пирамида (10) при p=ën/2û соответствует всем “висячим”, то есть не имеющим потомков, вершинам (см. лемму 1 при s=2).

Если последовательность (8) - пирамида, то

v₀ = max(v₀, v₁, ... , v_n_-1). (11)

Последовательность (8), представленная в виде бинарного дерева, является пирамидой тогда и только тогда, когда значение любого узла j дерева не меньше значений его возможных левого и правого потомков: 2×j+1 и 2×j+2.

Пример. Последовательность

23, 20, 11, 13, 8, 9, 8, 11, 10, 7, 1

является пирамидой. Наглядно это видно на рис.2.

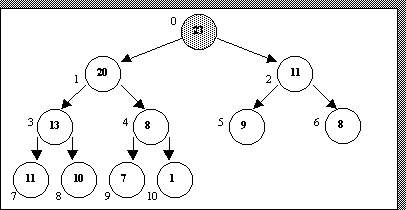
Рис. 2. Пирамида, представленная в виде бинарного дерева

Теперь можно приступить к описанию алгоритма пирамидальной сортировки. Состоит он в реализации двух этапов. Остановимся на них подробнее.

Этап 1. Построение пирамиды. В массиве (8) “хвост”, то есть подпоследовательность (10) при p = ën/2û , как мы уже отмечали, является пирамидой. Будем наращивать (10), добавляя к ней оставшиеся элементы из (8). Пусть последовательность v_j+1, v_j₊₂, ... , v_n-₁ - уже пирамида. Припишем к ней слева элемент v_j:

v_j, v_j₊₁, ... , v_n-₁ (12)

и преобразуем (12) снова в пирамиду. Для этого “просеем” v_j по соответствующей веточке двоичного представления (8). Делаем это так. Рассмотрим v_j и два его возможных потомка: v_2×j+1 и v_{2×j +2}. Если v_j не меньше потомков или не имеет их, то вычисления прекращаем. В противном случае обмениваем значения v_j и max(v_{2×j + 1}, v_{2×j +2}) в соответствующих позициях дерева и “опустившийся” элемент продолжаем просеивать тем же самым способом. В конце концов, преобразованная последовательность (12) станет пирамидой. Продолжая наращивание (12), мы превратим весь массив (8) в пирамиду. При этом окажется выполненным равенство (11). Объявляем полученную пирамиду S текущей и переходим к следующему этапу.

Этап 2. Сортировка пирамиды. В текущей пирамиде T начальный элемент не меньше остальных. Поступим с ним так. Обменяем значениями концевые (начальный и конечный) элементы T и укоротим T справа на один элемент. Полученная последовательность уже может и не быть пирамидой. Применим в ней к элементу v₀ процесс “просеивания”, описанный на этапе 1. Преобразованная последовательность становится пирамидой. Повторяя этот этап (n-1) раз, отсортируем T по неубыванию.

адача 5. Составить рекурсивную программу бинарной пирамидальной сортировки массива, заданного вектором v = (v₀ v₁ ... v_n_-1).

Решение. Описанный выше алгоритм пирамидальной сортировки реализуется функциями shift(), build(), sortpiram() и piramida().

Вспомогательная рекурсивная функция shift(v, b, e) просеивает в векторе v компонент от позиции b и не далее чем до позиции e или, при представлении v в виде бинарного дерева, от вершины b до вершины e. При этом используется такой алгоритм. Если значение в b не меньше значений в вершинах-потомках, то вычисления прекращаются. В противном случае своими значениями обмениваются b и потомок с наибольшим значением. Если имеются два претендента на обмен с b, то берется потомок с меньшим номером. Далее задача рекурсивно решается на новом участке [b, e] c измененным значением индекса b (b¬2×b+1 или b¬2×b+2). Базой рекурсии является условие 2×b+1>e. Декомпозиция организуется по длине участка [b, e]. Функция shift(v, b, e) в дальнейшем будет использоваться для восстановления в векторе v пирамиды на [b, e] при условии, что свойства пирамиды на этом участке нарушены только в вершине b.

Рекурсивная функция build(v, k, e) на участке [0, e] строит в векторе v пирамиду. Предполагается, что на участке [k+1, e] в v пирамида уже построена. Рекурсия организована по параметру k.

Рекурсивная функция sortpiram(v, e) на участке [0, e] в векторе v сортирует ранее построенную пирамиду по неубыванию. Рекурсия организована по параметру e.

Головная функция piramida(v), используя функции build() и sortpiram(), строит из вектора v пирамиду, а затем сортирует её по неубыванию:

(13)

(14)

(15)

(16)

Контрольный пример:

Анализ пирамидальной сортировки показывает, что для её выполнения требуется не более 3×(n-1)×log₂(n) элементарных операций типа сравнений и обменов (см. главный член в оценке леммы 3 при s=2). Подобная эффективность, реализация без дополнительной памяти и гарантированная надежность для худшего случая часто оказываются решающими факторами, заставляющими в конкретных ситуациях отдавать предпочтение именно этому способу сортировки.

Замечания.

Если в функции shift() неравенства v_k< v_k+1 и v_b< v_k заменить соответственно на v_k> v_k+1 и v_b> v_k, то функция piramida2() будет осуществлять сортировку по невозрастанию;

Незначительные изменения приведенных функций позволяют получить достаточно компактный нерекурсивный вариант алгоритма бинарной пирамидальной сортировки. Это будет сделано в следующем пункте для более общей задачи.