В основах анализа [40, с. 17- 38] операции сложения и умножения над натуральными числами определяются рекурсивным способом, опираясь на аксиомы Пеано о “существовании последующего числа” и “индукции”. Первая из названных аксиом звучит так: “Для каждого натурального x имеется и притом только одно натуральное число, называемое его последующим и обозначаемое число x¢ ”. Постараемся промоделировать указанные выше и некоторые иные операции.

адача 42. Для целых неотрицательных чисел n, m разрешены операции: нахождения последующего числа (n+1) и предыдущего числа n-1 (n>0). Промоделировать с помощью рекурсивных функций операции нахождения суммы (n+m), разности (n-m (n³ m)), умножения (n× m), возведения в степень n^m (n>0), частного и остатка при делении n на m (n/m).

A. Сумма: a+b. Очевидное соотношение

задает одновременно и базу рекурсии и правило декомпозиции. По нему и построена следующая рекурсивная программа-функция:

Контрольный пример: plus(5,7) = 12.

B. Разность: a-b (a³b). В данном случае база рекурсии и декомпозиция могут быть извлечены из соотношения

Соответствующая рекурсивная программа-функция выглядит так:

Контрольный пример: minus(30,13) = 17.

C. Умножение: a× b. Будем считать, что операция сложения уже определена. Тогда соотношение, из которого легко извлекаются рекурсивная база и декомпозиция, для данного случая выглядит следующим образом:

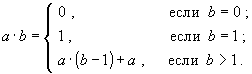
Соответствующая рекурсивная программа-функция может быть записана, например, так:

Контрольный пример: multi(3,7) = 21.

D. Возведение в степень: a^b (a ¹ 0). Будем считать, что операция умножения уже определена. Тогда:

и рекурсивная программа-функция возведения в степень может быть задана так:

Контрольный пример: power(2,5) = 32.

E. Частное и остаток: a/b (b > 0). В данной задаче речь идет об отыскании величин q и r из представления a=q×b+r (0£r<b, q³0). Будем предполагать, что операция вычитания уже определена, а ответ должен быть возвращен в виде вектора с двумя компонентами: (q    r)^T. Если a<b, то q=0 и r=a. Этот факт и определяет базу рекурсии. Если же b>a, то a/b=1+(a-b)/b, что позволяет организовать декомпозицию. Все сказанное учтено в рекурсивной функции divi(q,a,b). В ней первый аргумент q является вспомогательным параметром. При обращениях к divi() он должен определять базовое значение частного, то есть быть равен нулю. Однако проще решать задачу с помощью вспомогательной функции div(a,b), возлагая на неё решение вопроса о правильном значении вспомогательного параметра при вызовах divi(). Это довольно типичный случай при обобщениях исходной задачи за счет введения дополнительных параметров:

Контрольный пример: div(222,50)^T = [4    22].

Замечание. Моделирование различных операций возможно не только для целых неотрицательных чисел. Их можно было бы определить и для множества всех целых чисел, и даже для множества вещественных чисел. Ограничимся рассмотрением одного примера. Напишем рекурсивную программу-функцию нахождения дробной части вещественного числа, если разрешены лишь операции x+1 и x-1. Вот один из возможных достаточно ясных вариантов её определения:

Контрольные примеры: fraction(3.72) = 0.72,     fraction(-3.72) = 0.28.