Латинские квадраты имеют длинную историю, восходящую к Л.Эйлеру. Они возникают в задачах теории групп и полугрупп, кодирования, составления расписаний, распределения ресурсов, очередности инициирования событий, выдачи студентам заданий и т.п. [55, c.261-282]. В настоящее время латинские квадраты опять становятся объектом активных исследований в связи с нерешенными проблемами конечных геометрий.

Определение. Латинским квадратом порядка n называют квадратную матрицу m размером n´n, элементы которой принадлежат множеству M = {1, 2, ..., n}, причем каждое число из M встречается ровно один раз в каждой строке и в каждом столбце m.

Из определения латинского квадрата вытекает, что строки m состоят из различных перестановок чисел от 1 до n. Столбцы m также состоят из различных перестановок этих чисел.

В качестве примера, приводящего к латинским квадратам, рассмотрим упрощенную задачу о составлении расписания. Пусть пять преподавателей P_i ( i = 1, 2, ..., 5) школы в течение пяти последовательных уроков должны провести занятия в пяти классах K_j ( j = 1, 2, ..., 5). При этом каждый из преподавателей обязан дать один урок в каждом классе. В этой ситуации оказывается, существует 1344 возможных различных расписаний. Ниже приведено одно из них:

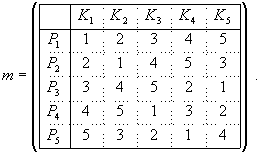
Элементы m интерпретируются здесь так. Преподаватель P_i ( i = 1, 2, ..., 5) проводит занятия в классе K_j ( j = 1, 2, ..., 5) на уроке номер m_i,j.

Ниже на основе алгоритма перебора с возвратом будут построены рекурсивные функции подсчета общего количества и генерирования совокупности латинских квадратов размером n´n. При этом в качестве строительного материала для их получения будет использоваться последовательность P всех перестановок из элементов {1,2,…,n}, представленная в лексикографическом порядке.

Напомним, что лексикографический порядок на P вводится так. Пусть

<a₀, a₁, ..., a_n-1>, <b₀, b₁, ..., b_n-1>ÎP

и для знака лексикографического сравнения перестановок используется символ <’ (меньше). Тогда считают, что:

<a₀, a₁, ..., a_n-1>, <' <b₀, b₁, ..., b_n-1> Û   $ (0 £ k £ n-1) [(a_k < b_k) Ù"(s < k)(a_s = b_s)].

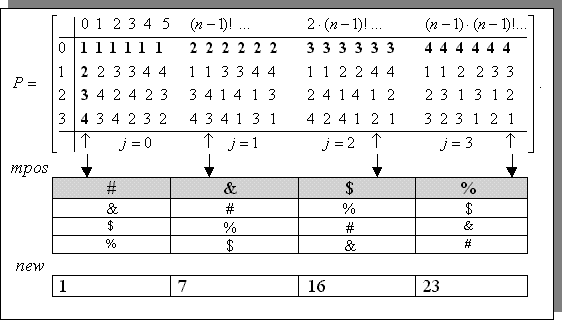
На рисунке 4 по столбцам в лексикографическом порядке выписаны все перестановки для n=4. В общем случае формировать их можно с помощью специальной рекурсивной функции (см. раздел “Перестановки”). При лексикографической форме записи последовательность перестановок P представляется в виде отдельных блоков по (n-1)! элементов в каждом. Если пронумеровать эти блоки от 0 до (n-1), то все перестановки блока j (j = 0, 1, …, n-1) будут начинаться с цифры (j+1). В дальнейшем этот факт будет использован при организации рекурсии.

Можно считать, что элементы нулевой строки любого формируемого латинского квадрата L есть последовательные цифры от 1 до n. При этих соглашениях j-й столбец для L есть просто одна из перестановок j-го блока P (j = 0, 1, …, n-1). Следовательно, возможен такой механизм формирования или подсчета количества всех латинских квадратов размером n´n.

Рис. 4. Схема формирования латинского квадрата из перестановок

1. Строим очередную матрицу-кандидат L, формируя каждый её j-й столбец из какой-либо перестановки j-го блока P (j = 0,1,…,n-1). Если L является латинским квадратом, то запоминаем или выводим его.

2. Если перебраны не все матрицы-кандидаты, то возвращаемся к пункту 1, иначе организуем вывод результата (если требуется) и вычисления прекращаем.

Подобный полный перебор всех возможных кандидатов весьма трудоемок. Однако предложенную схему вполне можно использовать для организации перебора с возвратом, сразу же отметающим многих кандидатов до их полного построения. Это и сделано ниже.

адача 5. Количество латинских квадратов. Написать рекурсивную программу-функцию, которая при заданном натуральном n методом перебора с возвратом подсчитывает количество латинских квадратов размером n´n с первой строкой вида: 1, 2, …, n.

Решение. Пусть P - последовательность перестановок в лексикографическом порядке из элементов {1,2,…,n} с n выделенными блоками (см. выше). Функции Lanum(n) и Latinu(n,fa,mpos,ot,j) решают поставленную задачу.

Головная функция Lanum(n) по заданному n подготавливает фактические аргументы для рекурсивной функции Latinu():

Параметры функции Latinu(n,fa,mpos,ot,j) имеют следующий смысл:

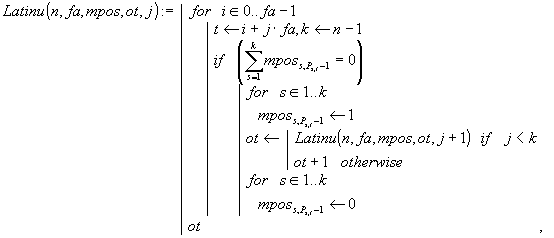
Остановимся подробнее на алгоритме, реализуемом функцией Latinu(), и динамике заполнения матрицы mpos нулями и единицами. На рисунке 4 из методических соображений в mpos вместо реальных единиц проставлены заменяющие их символы: #, &, $ и %. Это дает возможность наглядно проследить за соответствием фиксируемых перестановок в каждом из блоков P и заполнением mpos единицами.

Прежде всего, отметим, что рекурсия организована по номеру j текущего блока P, из которого и выбирается очередной столбец для создаваемого латинского квадрата L. Пусть мы находимся в j-м рекурсивном вызове, то есть для построения L уже выбраны перестановки из 0,1,…, (j-1)-го блоков P и зафиксирован некоторый столбец t из j-го блока P. По отдельности рассмотрим такие возможные взаимоисключающие случаи:

A. Позиции (s, P_s,t - 1) (s = 0, 1, ..., n-1) матрицы mpos установлены в нуль (сумма соответствующих элементов равна нулю):

mpos_s,Ps,t-1 := 0   (s = 1, 2, ..., n-1) или .

B. По крайней мере, одна из позиций (s, P_s,t - 1) (s = 1, 2, ..., n-1) матрицы mpos установлена в единицу.

Пусть справедливо утверждение A. Тогда выполняются следующие действия. Позиции (s, P_s,t - 1) (s = 1, 2, ..., n-1)матрицы mpos переустанавливаются в единицу:

mpos_s,Ps,t-1 := 1   (s = 1, 2, ..., n-1)

и столбец j подсоединяется к формируемому квадрату. Далее, если j < n-1, то осуществляется переход к следующему рекурсивному вызову, иначе очередной латинский квадрат уже построен и величина ot увеличивается на единицу. После увеличения ot (или возврата из рекурсивного вызова) элементы mpos, установленные в данном рекурсивном вызове в единицу, переустанавливаются в нуль. Это дает возможность продвигаться дальше по текущему блоку P в поисках очередного столбца для L.

Пусть справедливо утверждение B. Тогда выполняются такие действия. В текущем j-м блоке P осуществляется переход к следующему столбцу, как к очередному кандидату на включение в L, и снова реализуется одна из альтернатив A или B. Если j > 0 и j-й блок P исчерпан, то осуществляется возврат из текущего рекурсивного вызова. После этого элементы mpos, установленные в (j-1)-м рекурсивном вызове в единицу, переустанавливаются в нуль. Если j=0 и j-й блок P исчерпан, то функция Latinu() возвращает вычисленное значение ot.

 Замечание. Рассматриваемую задачу можно было бы решать более эффективно. Например, так. Пусть функция Latinu() формирует лишь латинские квадраты с нулевой строкой и нулевым столбцом вида 1, 2, …,n. Если их количество окажется равным m, то решением задачи, очевидно, будет число m×(n-1)!. Для реализации этой схемы достаточно зафиксировать начальную перестановку нулевого блока P и не изменять её в процессе вычислений, что соответствует организации рекурсии не с нулевого, а с первого блока P. Добиться этого можно следующей незначительной модификацией функции Lanum():

Контрольные примеры. В таблице указано количество латинских квадратов для значений n от двух до шести. Расчет проведен по функции Lanumq(n).

адача 6. Латинские квадраты. Написать рекурсивную функцию, которая при заданном натуральном n формирует и выводит латинские квадраты размером n´n с нулевой строкой и нулевым столбцом вида: 1, 2, …, n.

Решение. При указанных в условиях задачи соглашениях j-й столбец любого формируемого латинского квадрата L должен выбираться из j-го блока матрицы перестановок P (j=0,1,…n-1). При этом нулевой столбец L всегда должен совпадать с нулевым столбцом нулевого блока P. В целях экономии памяти ответ будем формировать в виде матрицы ot, каждый столбец k (k=0,1,…) которой кодирует конкретный латинский квадрат L по такой схеме. Значение элемента ot_i,k (i = 0, 1, ..., n-1) - это номер i-го столбца L в матрице P (см. рис.5).

Решением задачи могут служить функции Latin() и Lainitq(). Вычисления по ним проводятся почти так же, как и по паре ранее рассмотренных функций Latinu() и Lanumq(). Основные отличия здесь следующие. Функция Latin() по сравнению с Latinu() имеет дополнительный формальный параметр-вектор new. Он служит для покомпонентного запоминания кода очередного формируемого латинского квадрата L в виде последовательных номеров столбцов P. Каждый вновь сформированный вектор new подсоединяется справа к матрице ответов ot (в Latinu() ot была простой переменной). Рекурсия в функции Latin() организована, как и в функции Latinu(), по номеру j текущего блока матрицы перестановок P.

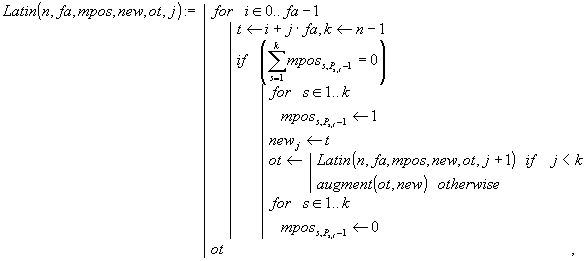
 Контрольные примеры. Ниже вычислено значение функции Lainitq(4) и справа от полученной матрицы приведены соответствующие её столбцам латинские квадраты.

Рис. 5. Соответствие столбцов матрицы ответов и латинских квадратов

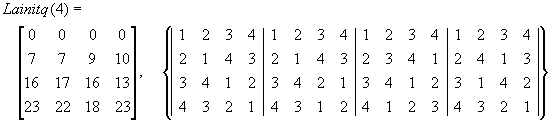
Замечание. Чтобы функция Latin() при заданном натуральном n вычисляла все латинские квадраты размером n´n с нулевой строкой вида: 1, 2, … , n и без ограничений на нулевой столбец, достаточно слегка модифицировать головную программу Lainitq(). Её новая редакция может быть такой: