адача 44. Разбиение многоугольника. Написать рекурсивную программу-функцию, подсчитывающую количество способов разбиения выпуклого многоугольника на треугольники непересекающимися диагоналями.

Решение. Пусть задан произвольный выпуклый n-угольник M(n) с вершинами, последовательно именованными против часовой стрелки от M₁ до M_n включительно. Обозначим через g_n искомое число разбиений M(n) на треугольники.

1. Рассмотрим (n+1)-угольник M(n+1) c вершинами M_k (k = 1, 2, ..., n+1) и зафиксируем одну из его сторон, например M₁M₂ . При любом разбиении M(n+1) найдется треугольник M₁M₂M_k, содержащий эту сторону. Возможны лишь три случая (см. рис. 10): M_k - вершина, соседняя с M₁ (k=n+1): M_k- вершина, соседняя с M₂ (k=3); M_k не является соседней вершиной ни с M₁, ни с M₂ (k=4, 5, …, n). Каждый случай разберем отдельно.

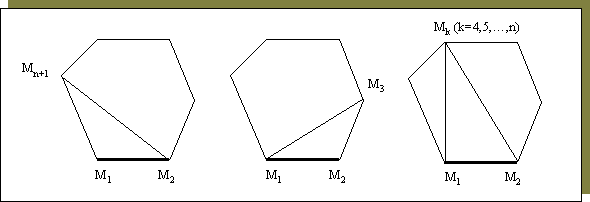
Рис. 10.  Возможные типы треугольников со стороной M₁M₂.

A.  M_k - вершина, соседняя с M₁ (k = n+1). Если из M(n+1) удалить треугольник M₁M₂M_k, то получим некоторый n-угольник, для которого, по предположению, существует g_n разбиений. Поэтому столько же разбиений будет существовать и для M(n+1).

B.  M_k - вершина, соседняя с M₂ (k = 3). Разбор проводится аналогично предыдущему случаю.

C.  M_k не является соседней вершиной ни с M₁, ни с M₂ (k = 4, 5, ..., n). Треугольник M₁M₂M_k разделяет M(n+1) на три части: сам M₁M₂M_k, (k-1)-угольник и (n-k+3)-угольник. Две последние из них примыкают к сторонам треугольника M₁M₂M_k и, по предположению, разбиваются на треугольники соответственно g_k-1 и g_n-k+3 способами. Следовательно, для данного k это дает g_k-1×g_n-k+3 способов разбиения M(n+1).

Учитывая подсчеты, проведенные в пунктах A, B и C, получаем:

                                                                 (19)

 В принципе, рекуррентная формула (19) уже пригодна для нахождения решений задачи: g₃ = 1, g₄ = 2, g₅ = 5, g₆ = 14 ... . Она же может служить основой и для составления соответствующей рекурсивной функции g(n). Но вычисления по такой функции g(n) будут неэффективны. Поэтому продолжим наши рассуждения, стараясь, по возможности, упростить (19).

2. Покажем, что число диагоналей, участвующих в любом конкретном разбиении многоугольника M(n), не связано со способом его разбиения и всегда равно n-3. Действительно, при любом разбиении образуется (n-2) треугольников. Число их сторон равно 3×(n-2). Если отсюда вычесть n (количество сторон M(n)) и учесть, что каждая диагональ - общая сторона двух соседних треугольников, то общее количество диагоналей разбиения будет равно (3×(n-2)-n)/2=n-3.

3. Пусть вершины M₁ и M₂ сливаются. При этом (n+1)-угольник превращается в n-угольник, а треугольник M₁M₂M_k - в отрезок: в сторону - для случаев A и B и в диагональ - для случая C. Теперь сумма слагаемых правой части (19), не считая 2×g_n, выражает число всех разбиений M(n), в которых участвует какая-либо диагональ, проходящая через фиксированную вершину (M₁=M₂). Сумма этих сумм по каждой из вершин дает значение Как это выражение связано с g_n? Во-первых, в нем каждая диагональ, проходя через две вершины, учтена дважды, а во-вторых, каждое разбиение M(n) подсчитано столько раз, сколько диагоналей участвует в этом разбиении, то есть n-3. Следовательно,

Из данного соотношения и (16) получаем:

Эту рекуррентную формулу уже вполне можно использовать для составления рекурсивной программы-функции g(n) решения задачи. Выглядеть она может, например, так:

 g(4) = 2,        g(5) = 5,        g(6) = 14,        g(10) = 1430,       

 g(20) = 477638700,           g(30) = 263747951750360.        

Замечание. Из выведенного ранее рекуррентного соотношения для g_n+1 достаточно просто получить и конечную формулу:

Значения g_n, получаемые по этой формуле, называются числами Каталана. Впервые они появились в исследованиях Э. Каталана в 1838 году и довольно часто и неожиданно возникают при решении разных задач, которые на первый взгляд мало связаны между собой.